SVX日記
2017-12-07(Thu) タートルグラフィックスを実装
先日に引き続き、ちょっとした用途のため、自製グラフィックライブラリにタートルグラフィックスの関数を追加することにした。習作として、フラクタル図形を描画するプログラムも書いてみる。やり始めたら極めてアッサリと、併せて数時間でできてしまった。
def c_curve(win, n, l)
unless(n == 0)
win.tLeft(45)
c_curve(win, n - 1, l)
win.tRight(90)
c_curve(win, n - 1, l)
win.tLeft(45)
else
win.tForward(l)
end
end
win.tHome
win.tRight(90)
c_curve(win, 12, 4) def r_dragon(win, n, l)
unless(n == 0)
win.tLeft(45)
r_dragon(win, n - 1, l)
win.tRight(90)
l_dragon(win, n - 1, l)
win.tLeft(45)
else
win.tForward(l)
end
end
def l_dragon(win, n, l)
unless(n == 0)
win.tRight(45)
r_dragon(win, n - 1, l)
win.tLeft(90)
l_dragon(win, n - 1, l)
win.tRight(45)
else
win.tForward(l)
end
end
win.tHome
win.tRight(90)
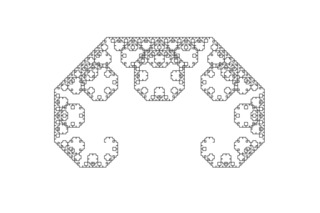
r_dragon(win, 12, 4) def tree(win, n, l)
unless(n == 0)
win.tSetPenWidth(n * 2)
win.tForward(l)
win.tRight(25)
tree(win, n - 1, l / 1.5)
win.tLeft(55)
tree(win, n - 1, l / 1.3)
win.tRight(30)
win.tBack(l)
else
win.tForward(l)
win.tBack(l)
end
end
win.tHome
tree(win, 7, 96)2017-12-16(Sat) パーフェクト破線描画ライブラリを実装
自由な曲線を、意図した通りに制御しつつ描くためにはベジェ曲線が最適だ。それは角丸の長方形を描くためにも有用。破線も描きたい。しかも、一点鎖線も二点鎖線も、開始点も終止点も、線が直角に曲がっても破綻しない破線が。
というわけで、先日のタートルグラフィックスに、パーフェクトなベジェ曲線と破線描画機能を実装してみた。文法は以下。
tThrough(終止点への角度, 終止点への距離, 終止点からの角度, {オプション})4.times { tThrough(45, 141.421356, 45) }ちょっと調べた限り、タートルグラフィックスにベジェ曲線を実装した事例は多くないようだが、その中でも、我ながらもっともシンプルかつ美しい実装方法であると自負している。オプションを与えることで、制御点までの距離や、破線のパターン等も指定できる。
# ベジェ曲線テスト
win.tSetPos(64, 64)
win.tSetHeading(90)
win.tArc(360, 4)
win.tForward(100)
win.tArc(360, 4)
2.times {
win.tThrough( 45, sqrt(120 ** 2 + 120 ** 2), -45)
win.tArc(360, 4)
win.tThrough(-45, sqrt(120 ** 2 + 120 ** 2), 45)
win.tArc(360, 4)
}
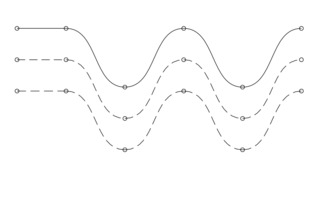
# 波線テスト
[false, true].each {|fit|
win.tSetPos(64, fit ? 192 : 128)
win.tSetHeading(90)
win.tArc(360, 4)
win.tDForward(*win.fit_dline(100, [0, [20, 10]], { :FIT => fit }))
win.tArc(360, 4)
2.times {
win.tDThrough( 45, sqrt(120 ** 2 + 120 ** 2), -45, { :PAT => [0, [20, 10]], :DIVS => 16, :FIT => fit })
win.tArc(360, 4)
win.tDThrough(-45, sqrt(120 ** 2 + 120 ** 2), 45, { :PAT => [0, [20, 10]], :DIVS => 16, :FIT => fit })
win.tArc(360, 4)
}
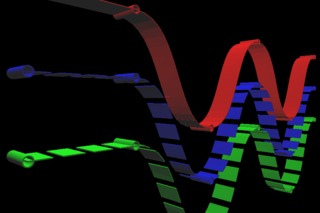
}で、ちょいとライブラリをOpenGL版に入れ替え、意味もなく3Dにしてグリグリと回してみたり。
思い返せば、このライブラリの原型を作ったのは10年以上前になるのか。こんなに長らく付き合うことになるとは思ってもみなかったな。
2017-12-25(Mon) クリスマス納車
20年以上前、初代ロードスターR-Limitedの新車購入をギリギリまで検討しながら、オープン志向が行き過ぎて裸の三菱ジープを選んでしまって以来、今年の6月に軽の自家用車を車検に出して以来、待ちに待った「赤いMTのオープンカー」を手にすることができた。
初めての新車購入で、ちょっと興味のあった「オドメータの初期値」は4km。ディーラーでひととおりの説明を受けてから帰宅し、予め購入してあったフロアマットとカップホルダを装着、ガソリンスタンドでハイオクを満タンにしてから、さっそくオープン状態で試運転に出発。








■ nekosan [来ましたね!!これからじっくり慣らしですか。 インパネ、タコメータが中央で大きく占めてるんですね。]
■ フルタニアン(管理者) [いやー、納車まで長かったです。 慣らしについてもいろいろ調べたんですが、ブン回して全力加速するのだけ、しばらく控え..]
■ nekosan [慣らしは、実はもう要らないといわれてて、実際、やらなくても大丈夫なんだろうなと思いつつ、どっちなんだろうなぁ?という..]
■ フルタニアン(管理者) [慣らしには諸説ありますが、クルマに踏めと言われた時は、割と素直に踏んじゃってますね……。 確かに暖気と似てます。暖気..]